SCHOLASTIC APTITUDE TEST 1999
MATHEMATICS
| Time: Two Hours |
Max. Marks: 60
|
- Answers must be written in English
or the medium of
instruction of the candidate in High school.
- Attempt all questions.
- Answer all the questions in the booklets provided
for the purpose. No pages should be removed from the
booklets.
- There is no negative marking.
- Answer all questions of section I at one place.
Same applies to section II. The remaining questions can
be answered in any order.
- Answers to sections I and II must be supported by
mathematical reasoning.
- Use of calculators, slide rule, graph paper and
logarithmic, trigonometric and statistical tables is not
permitted
Section
I
This section has 5
questions. Each question is provided with five alternative
answers. Only one of them is correct.
Indicate the correct answer by A or B or C or D or E. Order
of the questions must be maintained. (5x2=10 Marks)
- Let R be the set of all
real numbers. The number of functions
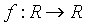 satisfying the
relation
satisfying the
relation 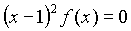 is
is
| A) Infinite |
B) One |
C) Two |
D) Zero |
| E) None of the above |
- a is a number such that the
exterior angle of a regular polygon measures 10a
degrees. Then
| A) there is no such a |
B) there are infinitely many
such a |
| B) there are precisely nine
such a |
D) there are precisely seven
such a |
| E) there are precisely ten such
a |
|
- f(n)=2f(n–1)+1
for all positive integers n. Then
A) 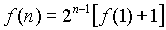 |
B) 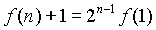 |
C) 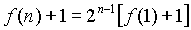 |
D) 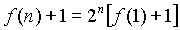 |
| E) None of these |
|
- For any
triangle let S and I denote the
circumcentre and the incentre respectively. Then SI
is perpendicular to a side of
| A) any triangle |
B) no triangle |
| C) a right angled triangle |
D) an isosceles triangle |
| E) an obtuse angled triangle |
|
- If f(x)=x3+ax+b
is divisible by (x-1)2 ,
then the remainder obtained when f(x) is divided
by x+2 is
| A) 1 |
B) 0 |
C) 3 |
D) –1 |
| E) None of these |
|
|
|
Section
II
This section has 5
questions. Each question is in the form of a statement with a
blank. Fill the blank so that the statement is true. Maintain the
order of the questions. (5x2=10 Marks)
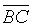 is a given line segment, H, K
are points on it such that BH=HK=KC. P is a
variable point such that
is a given line segment, H, K
are points on it such that BH=HK=KC. P is a
variable point such that
(i) 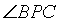 has
the constant measure of a radians.
has
the constant measure of a radians.
(ii) 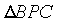 has
counter clockwise orientation
has
counter clockwise orientation
Then the locus of the centroid of 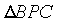 is the arc of the circle bounded
by the chord
is the arc of the circle bounded
by the chord 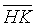 with angle in the segment ____________
radians.
with angle in the segment ____________
radians.- The coefficient of
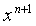 in
in 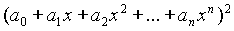 is __________
is __________
- n is a natural
number such that
i) the sum of its digits is divisible by 11
ii) its units place is non-zero
iii) its tens place is not a 9.
Then the smallest positive integer p such that 11
divides the sum of digits of (n+p) is
_____________
- The number of positive
integers less than one million (106) in which
the digits 5, 6, 7, 8, 9, 0 do not appear is
______________
- The roots of the
polynomial
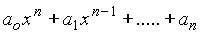 are all positive and are denoted by a i,
for i=1, 2, 3, ….., n. Then the roots
of the polynomial
are all positive and are denoted by a i,
for i=1, 2, 3, ….., n. Then the roots
of the polynomial
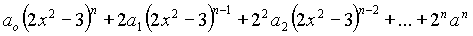 are, in
terms of a i, _________.
are, in
terms of a i, _________.
Section
III
This section has 5
questions. The solutions are short and methods, easily suggested.
Very long and tedious solutions may not get full marks. (5x2=10
Marks)
- Given any
integer p, prove that integers m and n
can be found such that p=3m+5n.
- E is the midpoint
of side BC of a rectangle ABCD and F
the midpoint of CD. The area of D AEF
is 3 square units. Find the area of the rectangle.
- If a, b, c are all
positive and c¹ 1, then prove that
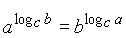
- Find the remainder
obtained when x1999 is divided by x2–1.
- Remove the modulus :
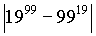
Section
IV
This section has 6
questions. The solutions involve either slightly longer
computations or subtler approaches. Even incomplete solutions may
get partial marks. (6x5=30 Marks)
- Solve the
following system of 1999 equations in 1999 unknowns :
x1+x2+x3=0,
x2+x3+x4=0…….,
x1997+x1998+x1999=0,
x1998+x1999+x1=0,
x1999+x1+x2=0
- Given base angles and the
perimeter of a triangle, explain the method of
construction of the triangle and justify the method by a
proof. Use only rough sketches in your work.
- If x and y
are positive numbers connected by the relation
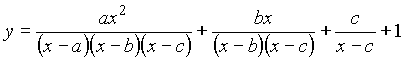 , prove
that
, prove
that
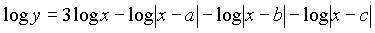
for any valid base of the logarithms.
- Let D
XYZ denote the area of triangle XYZ. ABC is a triangle. E,
F are points on
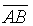 and
and 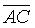 respectively.
respectively. 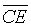 and
and 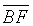 intersect in O. If D
EOB=4, D COF=8, D
BOC=13, develop a method to estimate D
ABC. (you may leave the solution at a stage where the
rest is mechanical computation).
intersect in O. If D
EOB=4, D COF=8, D
BOC=13, develop a method to estimate D
ABC. (you may leave the solution at a stage where the
rest is mechanical computation).
- Prove that 80 divides
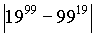
- ABCD is a convex
quadrilateral. Circles with AB, BC, CD, DA as a diameters
are drawn. Prove that the quadrilateral is completely
covered by the circles. That is, prove that there is no
point inside the quadrilateral which is outside every
circle.
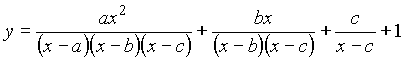 , prove
that
, prove
that