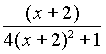SCHOLATIC APTITUDE TEST 1998
MATHEMATICS
| Time: Two Hours (8.30
AM - 10.30 AM)
|
Max. Marks: 60
|
NOTE:-
- Answers must be written in English
or the medium of
instruction of the candidate in High school.
- Attempt all questions.
- Answer all the questions in the booklets provided
for the purpose. No pages should be removed from the
booklets.
- There is no negative marking.
- Answer all questions of section I at one place.
Same applies to section II. The remaining questions can
be answered in any order.
- Answers to sections I and II must be supported by
mathematical reasoning.
- Use of calculators, slide rule, graph paper and
logarithmic, trigonometric and statistical tables is not
permitted
Section I
This section has 5 questions. Each question
is provided with five alternative answers. Only one
of them is correct. Indicate the correct answer by Aor B or C or
D or E. Order of the questions must be maintained. (5x2=10
Marks)
- p is the smallest positive such that every
positive integer greater than p can be written as
a sum of two composite numbers. Then
A) p=3 B)
p=6 C) p=10
D) p=11 E) None of these
- ABC is a triangle such that ma
> a/2, where ma = length
of the median through A and a = length of BC.
Then
| A)
such a triangle does not exist |
B)  A
is acute A
is acute |
C)  A is obtuse
A is obtuse |
D)  A
is right A
is right |
| E)
None of these |
|
- A vegetable shop keeps only four weights, one each of 1
kg, ½ kg, ¼ kg, 1/8 kg. A newly
appointed shop assistant claims that he has so far taken
once and only once each weighing possible with the
available weights. If n is the number of all
weighings possible and W the total weight of all
possible weighings, then
A) n=4,W=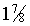 kg kg |
B) n=16,
W=30kg |
| C) n=15,W=15
kg |
D) n=15,
W=7.5 kg |
| E)
None of these |
|
 are the roots of the polynomial
are the roots of the polynomial 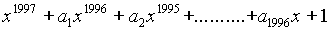 and
and 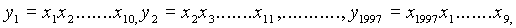 Then
Then 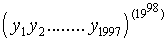 is
independent of
is
independent of
| A)
All ai |
B)
All ai, i ¹ |
| C)
None of ai |
D)
All ai ,i even |
| E)
All ai ,i odd |
|
- Triangle ABC is isosceles, right angled at B and has area
S. A circle is constructed with B as center and BA as
radius. A semicircle is constructed externally on
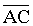 , that is, on
the side of AC which is opposite to that of B. Then the
area of the crescent or sickle formed between the circle
and the semicircle is
, that is, on
the side of AC which is opposite to that of B. Then the
area of the crescent or sickle formed between the circle
and the semicircle is
| A) 2S |
B) S/2 |
C) S |
D) 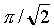 S S |
E)
None of these |
Section II
This section has 5 questions. Each question
is in the form of a statement with a blank. Fill the blank so
that the statement is true. Maintain the order of the questions.
(5x2=10 Marks)
- Numbers 1,2,3,…..,1998 are written in the
natural order. Numbers in odd places are stricken off to
obtain a new sequence. Numbers in odd places are stricken
off from this sequence to obtain another sequence and so
on, until only one term a is left. Then a=________
- S is the circumcircle of an equilateral triangle ABC. A
point D on S is such that C and D lie on opposite sides
of AB. Then
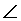 ADB=
radians
ADB=
radians
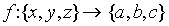 is a bijection from a 3-element set
into a 3-element set. It is given that exactly one of the
following statements A,B,C is true and the remaining two
are false: A:
is a bijection from a 3-element set
into a 3-element set. It is given that exactly one of the
following statements A,B,C is true and the remaining two
are false: A: 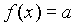 B:
B: 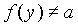 C:
C: 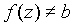 . Then
. Then 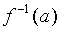 = .
= .- Given that x is real, the solution set of
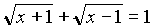 is
.
is
.
- In the standard expansion of
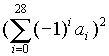 , the number of
terms appearing with -ve sign is
.
, the number of
terms appearing with -ve sign is
.
Section III
This section has 5 questions. The solutions
are short and methods, easily suggested. Very long and tedious
solutions may not get full marks. (5x2=10 Marks)
- Determine all positive integers n such that n+100
and n+168 are both perfect squares.
- Determine with proof whether integers x and y
can be found such that x+y and x2+y2
are consecutive integers.
- The first term of an arithmetical progression is Log a
and the second term is Log b. Express the sum to n
terms as a logarithm.
- p,q,r,s are positive real numbers. Prove that (p2+p+1)(q2+q+1)(r2+r+1)(s2+s+1)
³ 81pqrs
- With the aid of a rough sketch describe how you will draw
a direct common tangent to two circles having different
radii. (No formal proof is required).
Section IV
This section has 6 questions. The solutions
involve either slightly longer computations or subtler approaches.
Even incomplete solutions may get partial marks. (6x5=30 Marks)
- If x+y+z=0, then prove that
(x2+xy+y2)3
+ (y2+yz+z2)3
+ (z2+zx+x2)3
= 3(x2+xy+y2)
(y2+yz+z2)
(z2+zx+x2)
- Simplify
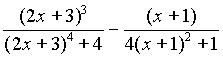 till it is obtained equal to
till it is obtained equal to 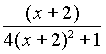
- a,b,c are distinct and p(x) is a polynomial
in x, which leaves remainders a,b,c on
division by x-a, x-b, x-c, respectively. Find the
remainder obtained on division of p(x) by (x-a)(x-b)(x-c).
- A point A is taken outside a circle of radius R. Two
secants are drawn from this point: One passes through the
center, the other at a distance of R/2 from the center.
Find the area of the circular region enclosed between the
two secants.
- A right angled triangle has legs a,b, a>b. The
right angle is bisected splitting the original triangle
into two smaller triangles. Find the distance between the
orthocenters of the smaller triangles using the co-ordinate
geometry methods or otherwise.
- If two sides and the enclosed median of a triangle are
respectively equal to two sides and the enclosed median
of another triangle, then prove that the two triangles
are congruent.
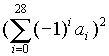 , the number of
terms appearing with -ve sign is
.
, the number of
terms appearing with -ve sign is
.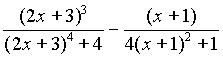 till it is obtained equal to
till it is obtained equal to