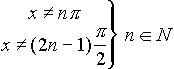
| A) |
B) |
C) |
D) None of these |
SCHOLASTIC APTITUDE TEST 1996
MATHEMATICS
| Time: Two Hours | Max. Marks: 60 |
| (8.30 AM - 10.30 AM) |
NOTE:-
PART-A
I. This section contains (7) questions. Each question has one or more than one correct answer(s). Indicate the answer(s) by A,B,C,D with brief reasoning. Order of the questions must be maintained. (7 x 2 =14 MARKS)
| A) n+1 is always a perfect square | B) n is never a perfect square |
| C) n is always divisible by 24 | D) n+12 is always a perfect square |
| A) All real values of x | B) No real value of x |
| C) All real values of x except x=0 | D) No real value of x except x=0 |
| E) All real values of x except x=1 | |
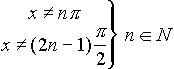
| A) |
B) |
C) |
D) None of these |
|
|
|
|
|
|
|
|
|
|
| A) n=4 | B) n=10 | C) n=12 | D) n=50 |
| A) not a function from X |
B) an one to one function
from X |
| C) an onto function of X |
D) R is a transitive relation on X |
II. This section contains (6) in-complete statements. complete the statements by filling the blanks. Write your answers in your answer book in the order in which the statements are given below. (6 x 2=12 MARKS)
i. If for some angle q and for some real number x it is given that sinq = x2-2x+2 then x should be equal to _______________ and q should be equal to ________________ degrees
ii. If a, b, c, d are four distinct integers between 1 to 10 such that for a traingle whose sides are in the ratios a:b:c, the altitudes are d:c:b. Then greatest of these four integers is _____________ and the smallest is __________________
iii. In a cylinder, AB is a diameter of the base circle and C is the centre of the top circle. Given that the volume of the cylinder is
cm3.
= 300, the perimeter of the traingle ABC is _____________ and the curved surface area of the cone with vertex C (having the same base) is ______________
iv. If the sum of the intercepts of the line with coordinate is 5 and the area of the traingle formed by the line and coordinate axes is 3 then intercepts are ______________________
v. In the figure given below
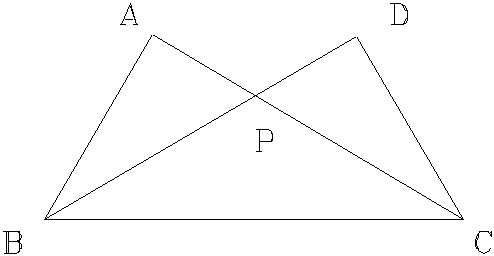
=
= 900 AP = 7.5 cm, AB = 10 cm, BC = 26 cm, Then CD is ________
vi.
Then a, b are __________________
III. This section contains (8) statements in GROUP-A and (4) questions in GROUP-B. Answer questions in GROUP-B on the basis of the statements made in GROUP-A. (4 x 1 = 4 MARKS)
GROUP-A
A,B and C are three distinct points in a plane .
i . There is no point D equidistant from A,B,C
ii. B lies on the perpendicular bisector of AC
iii. Among the three lengths AB, BC, AC the largest is the sum of the other two
iv. There is a point D such that ABCD is a rhombus
v. There is a point D such that ABCD is a rectangle
vi. In triangle ABC, the angular bisector B is perpendicular to the side AC
vii. AB is a tangent to the circle through B with centre C
viii. AC is a diameter of the circle passing through A, B, C.
GROUP-B
1. Which of the above statements mean that A, B, C are collinear
2. Which of the above statements mean AB = BC
3. Which of the above statements mean that AB is perpendicular to BC
4. Which of the above statements infer ABCD is cyclic quadrilateral
PART-B
IV. The numerator of a fraction is less than its denominator by 2. When 1 is added to both the numerator and denominator we get another fraction. The sum of these two fractions is
. Find the first fraction . (5)
V. Let
be the roots of the quadratic equation x2+ax+b=0 and
,
be the roots of the equation
x2-ax+b-2=0. Given that
and
= 24. Find the value of the coefficient a. (5)
VI. Find the number of points with integral coordinates in the cartesian plane satisfying the inequalities
|x|
100; |y|
100; |x-y|
100 (5)
VII. Given an
ABC of magnitude less than 1800 and O is a point inside it. Draw a straight line through O which forms a traingle with minimum perimeter. (Describe the construction and give proof). (5)
VIII. Perpendiculars are drawn from the vertex of the obtuse angle of a rhombus to its sides. The length of each perpendicular is equal to `a’ units. The distance between their feet being equal to `b’ units. Determine the area of the rhombus. (5)
IX. Let the sequence
be defined by
(a) u1 = 5 and the relation un+1 - un = 3 + 4(n-1) n
N
Express un as a polynomial in n.
(b) The remainder R, when x100 is divided by x2-3x+2, is a polynomial. Find x.(3)