SCHOLASTIC APTITUDE TEST -
1995.
MATHEMATICS
| Time: Two Hours |
Max. Marks: 60
|
| (8.30 AM - 10.30 AM) |
|
Answers must be written either in English or the medium of
instruction of the candidate in high school.
- There will be no negative marking.
- There are FIVE parts.
- Answer all questions of a part at one place.
- Use of calculators or graph papers is not permitted.
PART A
This part contains five statements. State whether the
statements are true or false. Give reasons.
(5 x 1 = 5 Marks)
- The product of three positive integers is equal to the
product of their L.C.M and G.C.D.
- 443 is prime number
- (a – b)x2 +(b – c)x
+(c – a) = 0 and (c – a)x2
+(b – c)x +(a – b) = 0
have a common solution for all real numbers a,b,c.
- Every odd number can be expressed as a difference of two
squares.
- The graph of
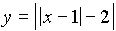 cuts the x-axis exactly once.
cuts the x-axis exactly once.
PART B
This part contains FIVE questions. Each question has only
one correct answer. Indicate your choice by marking with the
correct letter. Show your working in brief. (5 x 2 = 10 Marks)
- If a2+b2+c2 = D where a
and b are consecutive positive integers and c = ab,
then
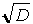 is
is
(A) always an even integer
(B) sometimes an odd integer and sometimes not
(C) always an odd integer
(D) sometimes rational, sometimes not
(E) always irrational
- A triangle ABC is to be constructed. Given side a (
opposite
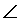 A ),
A ), 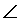 B and hc , the
altitude drawn from C on to AB. If N is the number of non-congruent
triangles then N is
B and hc , the
altitude drawn from C on to AB. If N is the number of non-congruent
triangles then N is
(A) one (B) two (C)
zero (D) zero or infinite (E)
infinite
- In any triangle ABC, a and b are the sides of triangle.
Given that
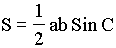 ( where S is the area of the
triangle), then
( where S is the area of the
triangle), then
A)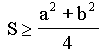 |
B)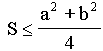 |
C)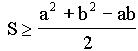 |
D)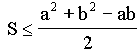 |
| E) None of these |
|
- If a0, a1, .............., a50
are respectively the coefficients of
 in
the expansion of
in
the expansion of 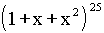 , then
, then  is
is
| A) odd |
B) even |
C) Zero |
D) None of these |
- The smallest value of
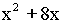 for all real values of x is
for all real values of x is
| (A) –16.25 |
(B) –16 |
(C) –15 |
(D) –8 |
(E) None of these |
PART C
This part contains FIVE incomplete statements. Complete the
statements by filling the blanks. Write only the answers in your
answer sheet strictly in the order in which the questions appear.
(5 x 2 = 10 Marks)
- The value of aÎ R for which the equation (1+a2)x2
+2(x-a)(1+ax)+1 = 0 has no real roots is
_______________________________.
- The greater of the two numbers 3114 and 1718
is _______________.
A and B are known verticies of a triangle.
C is the unknown vertex. P is a known point in the plane
of the triangle ABC. Of the two following hypotheses,
Hypothesis
I - P is the incentre of D ABC
Hypothesis
II - P is the circumcentre of D ABC.
The hypothesis which will
enable C to be uniquely determined is ____I / II____
(Strike off the inapplicable)
- If x = 0.101001000100001 ................ is
the decimal expansion of positive x, and in the series
expansion of x the first, second and third terms are
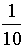
 ,
, 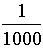 ,
and
,
and 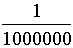 then the 100 th term is
_______________________.
then the 100 th term is
_______________________.
- If ABC is a triangle with AB = 7, BC = 9
and CA = n where n is a positive integer, then
possible two values of n are ____________________.
PART D
| Attempt any FIVE questions. |
(5 x 5 = 25 Marks)
|
- Solve the equations
xy + yz + zx = 12-x2 = 15-y2 = 20-z2
- A is 2 x 2 matrix such that AB = BA
whenever B is a 2 x 2 matrix. Prove that A must
be of the form kI, where k is a real number and I the identity
matrix
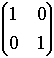 .
.
- Determine all 2 x 2 matrices A such that A2=I,
where I =
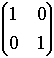 .
.
- Find an explicit formula ( in terms of nÎ N )
for f(n), if f(1)=1 and f(n)=f(n –1) + 2n – 1
- Let ABCD be a square. Let P,Q,R,S be respectively points
on AB,BC,CD,DA such that PR and QS intersect at right
angles. Show that PR=QS.
- Let ABC be any triangle. Construct parallelograms ABDE
and ACFG on the outside D ABC. Let P be any point where
the lines DE and FG intersect. Construct a parallelogram
BCHI on the outside D ABC such that PA and BI are equal
and parallel. Show that Area of ABDE + Area of ACFG =
Area of BCHI.
- A belt wraps around two pulleys which are mounted with
their centres s apart. If the radius of one pulley
is R and the radius of the other is (R+r) , show
that the length of the belt is
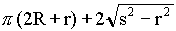 .
.
PART E
| Attempt any ONE question |
(1 x 10 = 10 Marks)
|
- Deduce pythogaras theorem from the result of problem 6 of
part D.
- Let x be any real number. Let
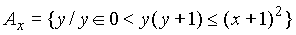 and
and 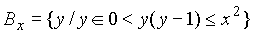 . Prove that
. Prove that 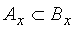 .
.
- Let
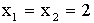 . Show
that there exists an infinite sequence
. Show
that there exists an infinite sequence 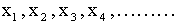 such that
such that 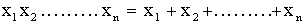 for all
positive integers n.
for all
positive integers n.
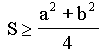
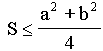
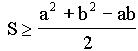
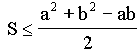
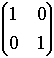 .
.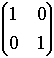 .
.