PHYSICS

Time: ONE Hour  Max. Marks: 60


  • Answers must be written either in English or the medium of instruction of the candidate in high school.
  • Answer all the questions in the booklets provided for the purpose.
  • There will be no negative marking.
  • The relevant working or the argument in arriving at an answer has to be included
    • in your answer.
  • Use of calculators or graph papers is not permitted.
  • Questions in Part A carry 6 marks each and questions in part B carry 3 marks each.
    •

Part A

(6x6=36 Marks)

  1. Two liquids of densities 1 g/cm3 and 3 g/cm3 are mixed in equal volumes. A cube of external dimension 20 cm has an inner cubical portion of side 10 cm whose density is twice that of the outer portion. If this cube is just floating in the liquid mixture, find the density of the inner portion. If the density of the inner portion is half of this value, what fraction of the volume of the cube will be submerged?
     
  2. A particle P is located at A. Another particle Q is located at B 200 m south of A. P starts moving at 2 m/s towards east at some moment and simultaneously Q starts moving at 4 m/s. (i) If Q moved first towards A and on reaching A quickly changed direction and moved towards east, find the time it takes to catch up with P. (ii) If instead Q aimed at a point C east of A at which it arrives at the same time as P, find the elapsed time. (iii) What should be the minimum speed of Q to catch up with P before it moves 50 m from its initial position? ( Assume Q catches up by aiming at the position P would reach at the same time as it does)
     
  3. A lens L1 produces a twice-magnified image of an object on a screen located 90 cm from the object. Without disturbing the object and the screen, another lens L2 of equal focal length is placed in contact with L1. This combination is adjusted to produce the image of the object on the screen again. What is the new magnification? (The two lenses together act as a single lens. The reciprocal of the focal length of the equivalent lens is equal to the sum of the reciprocals of the focal lengths of the individual lenses)
     
  4. Rate at which energy is received by a square meter of area facing the sun is 1400 Wm-2. Assume 50% efficiency for conversion of this energy in to heat and find the amount of time it takes for the temperature of 10 kg of water to rise through 10 C0 due to energy received by a 2m ´ 2m area. Assume the surface always faces the sun. How many kilowatt-hours of energy is this equal to? How long would a 40 W lamp glow if this energy were converted in to electrical energy at 25% efficiency.
     
  5. Fission of a nucleus of U235 releases about 250 MeV of energy. If 235 g of U235 is subjected to fission, find the energy (in joule) evolved in the process. Find the fraction of the mass of uranium that disappears in the fission process. (Assume 1 amu is 900 MeV for the purpose of calculation.)
     

  1. Waves reaching a point from two different paths from two different sources interfere. If the path lengths differ by integral multiples of a wavelength the interference will be constructive and if the path lengths differ by odd multiples of half wavelengths interference will be destructive. In the given situation waves travel from A to B along path 1 and path 2. If the frequency of the waves is n and the velocity of the waves is v, find the least difference between length of paths 2 and 1 that produces constructive interference at B. If the velocity along path 1 is v1 and along path 2 is v2, find the least difference between length of paths 2 and 1 that produces destructive interference at B.

Part B

(8x3=24 Marks)

  1. Two particles are moving round concentric circular paths of radii r1 and r2 (r2= 3r1) and are closest to each other at a certain moment. The particle on the outer path has slower speed v2 as compared to the inner one which has a speed v1 (v1=2v2). Find the least time interval between their successive appearances at their initial positions at the same time.

  1. A metal rod R tightly fits in to a ring as shown. Will there be any distortion in the ring on heating or cooling it? Discuss possible cases.

  1. An open room contains air (Assume air behaves as an ideal gas). Does the air in the room obey Charles law ()

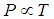  2. It is not as hot at some distance at the side of a flame as the same distance above it. Why is this so?

  3. The bob of a simple pendulum is made of metal. If a wooden bob replaces the metallic bob, how do the time periods of oscillations compare?

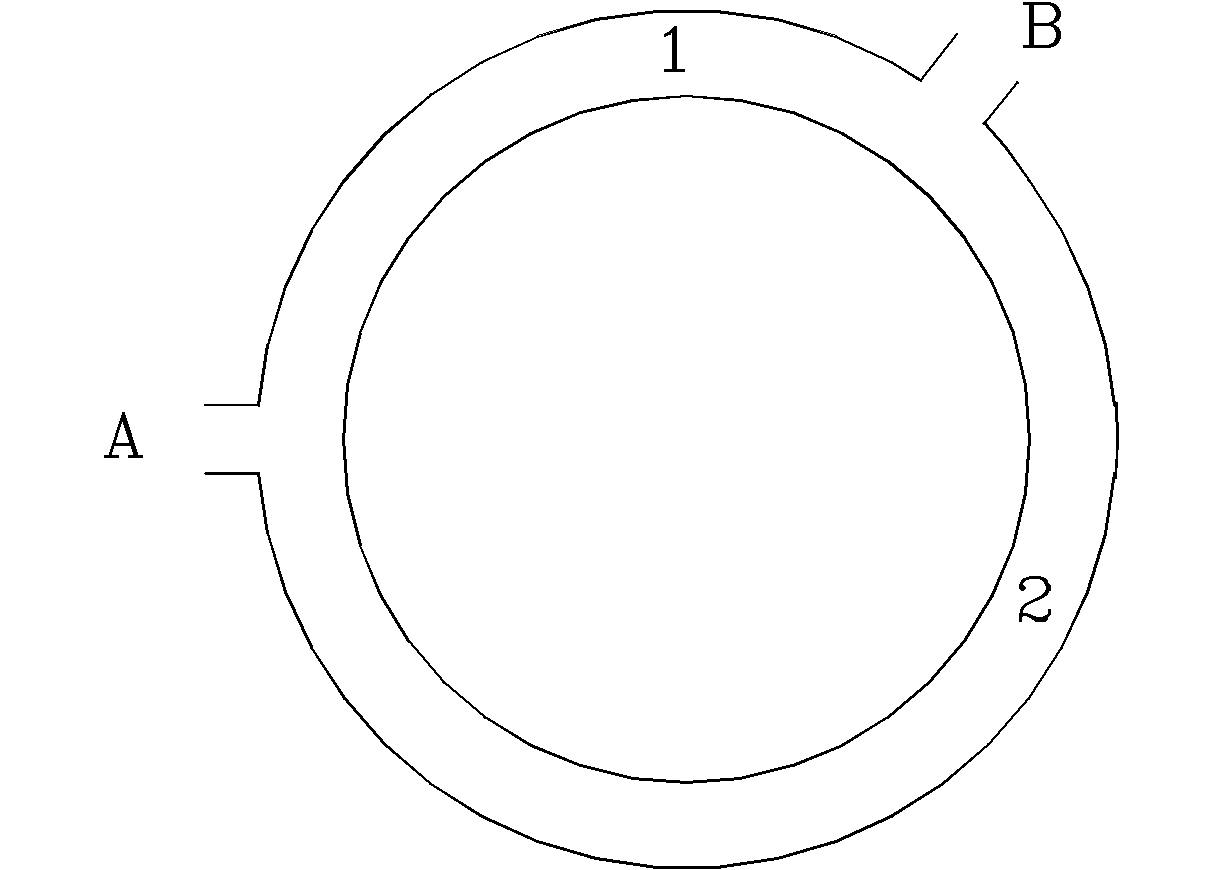
  4. A metallic vessel is placed on a non-conducting stand. The inner and outer surfaces of the vessel are connected to two gold leaf electroscopes A and B respectively. A charged sphere suspended by a non-conducting string is slowly lowered in to the vessel. How do the leaves of the electroscopes A and B behave? How will the behaviour change if the sphere makes contact with the inner surface of the vessel?

  5. A particle starts from rest and accelerates along a straight line at a1 for some time and then at a2 for an equal time covering a distance d1. If the acceleration for the first interval were a2 and for the second a1 the distance travelled is d2. How do the distances d1 and d2 compare? Support your answer either qualitatively or quantitatively.

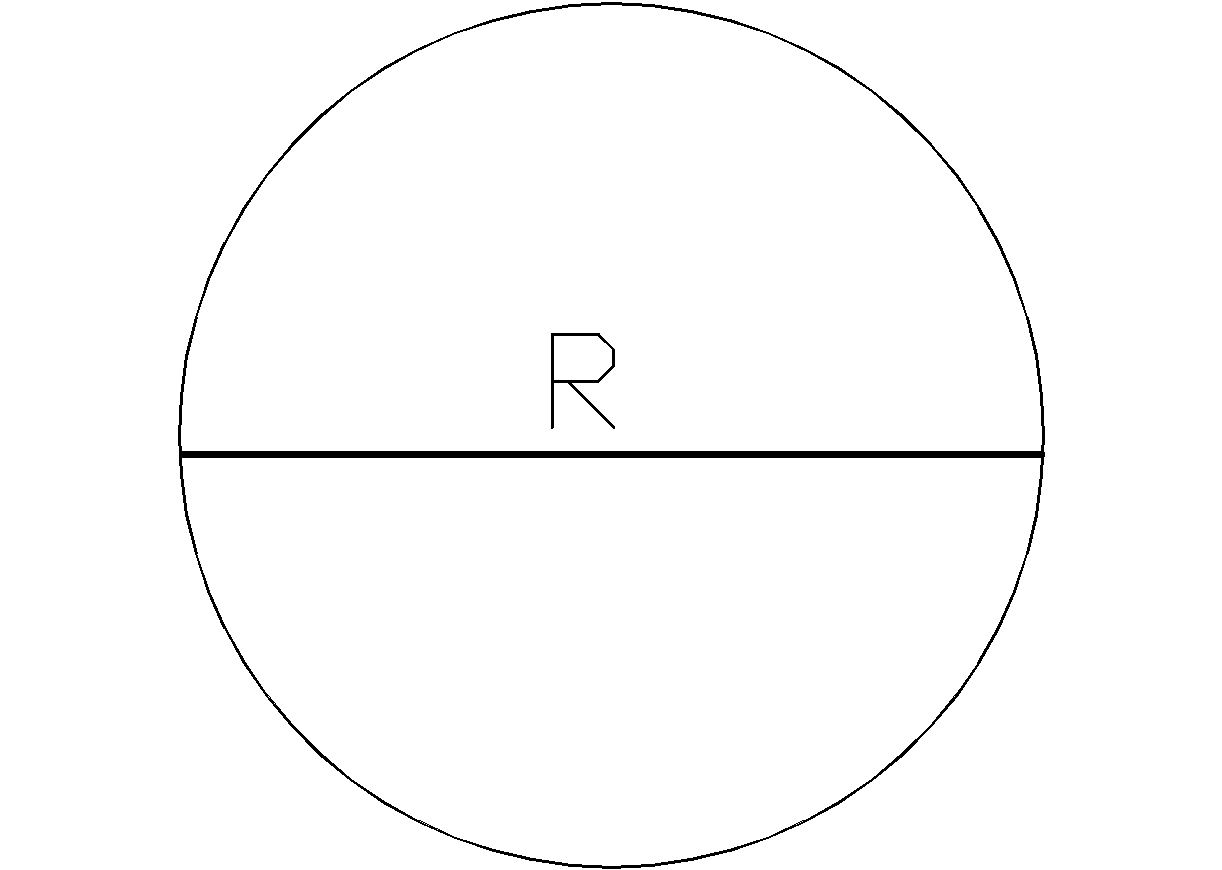
  6. A thin bar magnet of magnetic moment M is bent to form an arc of a circle making an angle q  (radians). Find its new magnetic moment.