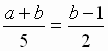1. Attempt all questions.
2. Answer to each question should begin on a fresh page, and rough work must be enclosed with answer book.
3. There is no negative marking.
4. Answer all parts of a question at one place.
5. Use of calculators, slide rule, graph paper and logarithmic, trigonometric and statistical tables is not permitted.

All answers to questions in Section-A, Section-B, Section-C must be supported by mathematical arguments. In each of these sections order of the parts must be maintained.

1. This section has Five questions. Each question is provided with five alternative answers. Only one of them is the correct answer. Indicate the correct answer by A,B,C,D,E.      (5×2=10 MARKS)

1. C is a circle with radius r. C₁, C₂, C₃, ....... C₂₀₀₃ are unit circles placed along the circumference of C touching C externally. Also the pairs C₁, C₂; C₂, C₃; ........ C₂₀₀₂, C₂₀₀₃; C₂₀₀₃, C₁ touch. Then r is equal to
A)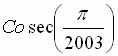
B)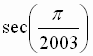
C)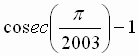
D)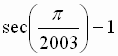
E) None of these

2. If n is a natural number, then 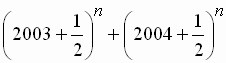is a positive integer

A) when n is even B) when n is odd C) only when n = 117 or n = 119 D) only when n = 1 or n = 3 E) none of these

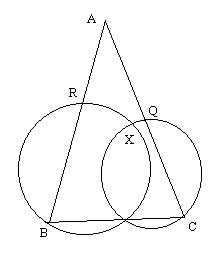
3. The line segment is completely external to a fixed circle S. A variable circle C through A, B moves such that it intersects S in distinct points P and Q. In one position of C, is parallel to . Then
A) there is precisely one more position of C such that is parallel to
B) is parallel to for infinitely many position of C and intersects for infinitely many positions of C.
C) is parallel to for all positions of C.
D) the hypothesis is wrong because there cannot be any position of C such that is parallel to E) None of these

4. f(x) is a polynomial of degree 2003. g(x) = f(x + 1) – f(x). Then g(x) is a polynomial of degree m, where
A) m = 2003 B) m = 2002 C) m cannot be uniquely determined, but
D) m may be undefined in some cases E) none of these

5. D PQR is the midpoint triangle of D ABC. Then both the triangles
A) have the same circumcentre B) have the same orthocenter
C) have the same centroid
D) are such that the circumcentre of the smaller triangle is the incentre of the bigger triangle
E) None of these

 

SECTION-B

2. This section has Five questions. In each question a blank is left.

Fill in the blank. (5×2=10 MARKS)

1. (m, n) is a pair of positive integers such that i) m < n, ii) their gcd is 2003, iii) m, n are both 4-digit numbers. The number of such ordered pairs is ________

2. In a triangle ABC, AB = 12, BC = 18, CA = 25. A semicircle is inscribed in D ABC such that the diameter of the semicircle lies on . If O is the centre of teh circle, then the length AO = ___

3. If x is the recurring decimal 0.037, then x^1/3 is the recurring decimal _____

4. The diagonals of a quadrilateral ABCD intersect in the point O. AO = OC. P is the midpoint of BD. Then D APB + D APD - D BPC - D DPC = _______

5. If x is any real number, then Int x stands for the unique integer n satisfying and Fr x stands for (x – Int x). If m is a positive integer, then = ______

 

SECTION-C

III. (4×2=8 MARKS)

1. Solve in positive integers m,n the equation 2^3m+1 + 3²ⁿ + 5^m + 5ⁿ = 2003

2. Given locations P, Q, R of the points of contact of the sides of a triangle ABC with its incircle, describe the procedure to construct triangle ABC.

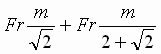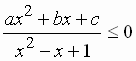3. The solution set of the inequation is {x / x is real and }. Determine a : b : c.

4. ABCD is a cyclic quadrilateral. bisects . AB = 10, AD = 12, DC = 11, Determine BC.

SECTION-D

IV. (3×4=12 MARKS)

1. To each of the first two of the 4 numbers 1, 19, 203, 2003 is added x and to each of the last two y. The numbers form a G.P. Find all such ordered pairs (x, y) of real numbers.

2. Show that the 4 points A, Q, X, R are concyclic in the following figure.

3. Factorize a(b² + c² – a²) + b(c² + a² – b²) + c(a² + b² – c²) – 2abc.

SECTION-E

(2×6=12 MARKS)

1. p is a plane. O is the origin. k > 0. is called a k-stretch of the plane if f_k(O) = 0 and for every f_k(A) is B where and OB = k.OA. P, Q are two points on the unit circle with origin as centre and PQ = 1. The plane is subjected alternatively to a 1/2-stretch and a 3-stretch, starting from the former. P and Q are transformed to P₂₀₀₃, Q₂₀₀₃ respectively at the end of the 2003rd stretch. Determine the distance P₂₀₀₃ Q₂₀₀₃.

2.
Determine the domain of f(x), in other words, determine the set of all real x for which f(x) is a real number. Sketch the graph of the function y = f(x). Determine from the graph the area of the region enclosed between the liens y = 0, x = 1 and x = 3 and the curve y = f(x).

SECTION-F

(1× 8=8 MARKS)

1. a and b are both 4-digit numbers a > b and one is obtained from the other by reversing the digits. Determine b if