MATHEMATICS
|
Time: Two Hours
(8.30 AM – 10.30 AM) |
Max.Marks:60
|
NOTE:-
- Attempt all questions.
- Answer to each question should begin on a fresh page, and rough work must be
enclosed with answer book.
- There is no negative marking.
- Answer all parts of a question at one place.
- Use of calculators, slide rule, graph paper and logarithmic, trigonometric
and statistical tables is not permitted.
Note:- All answers to questions in Section-A,
Section-B, Section-C must be supported by mathematical arguments. In each of these sections order of
the parts must be maintained.
SECTION-A
- This section has Five questions. Each question is provided with five
alternative answers. Only one of them is the correct answer. Indicate the
correct answer by A,B,C,D,E.
(5´ 2=10 MARKS)
1. Let m be the l.c.m. of 32002-1 and 32002+1.
Then the last digit of m is
| A) 0 |
B) 4 |
C) 5 |
D) 8 |
E) none |
Hint: Read off g.c.d. and hence determine the l.c.m.
2. In every cyclic quadrilateral ABCD with AB parallel to
CD
A) AD = BC, AC 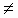 BD BD |
B) AD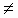 BC, AC BC, AC 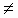 BD BD |
C) AD 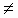 BC, AC = BD
BC, AC = BD |
D) AD = BC, AC = BD |
| E) none of these |
|
3. f,g,h:R R
are defined by f(x) = x-1, g(x) =
R
are defined by f(x) = x-1, g(x) = 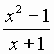 if x
if x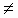 -1
h(x) =
-1
h(x) = 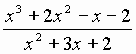 if x
if x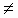 -1,
x
-1,
x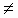 -2 -2 if x = -1 -2 if x = -1 -3 if x = -2
Then f(x) + g(x) – 2.h(x) is
-2 -2 if x = -1 -2 if x = -1 -3 if x = -2
Then f(x) + g(x) – 2.h(x) is
| A) not a polynomial |
B) a polynomial whose degree is
undefined |
| C) a polynomial of degree 0 |
D) a polynomial of degree 1 |
| E) none of these |
|
4. A, B are two distinct points on a circle with center C1
and radius r1. 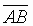 also
is a chord of a different circle with center C2 and radius r2.
S denotes the statement: The arc AB divides the first circle into two parts of
equal area.
also
is a chord of a different circle with center C2 and radius r2.
S denotes the statement: The arc AB divides the first circle into two parts of
equal area.
A) S happens if C1C2 > r2
B) If S happens then C1C2 > r2
C) If S happens then it is possible that C1C2
= r2
D) If S happens then it is necessary that C1C2
< r2
E) none of these
5. Triangle T1 has vertices at (-3,0), (2,0) and
(0,4). Triangle T2 has vertices at (-3,3), (3,5) and (1,-2). Plot
all points l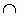 m where the line
segment l is a side of T1 and the line segment m is a side of T2,
whenever l
m where the line
segment l is a side of T1 and the line segment m is a side of T2,
whenever l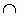 m is a unique point.
These points of intersection determine a convex polygon, which is a
m is a unique point.
These points of intersection determine a convex polygon, which is a
| A) triangle |
B) quadrilateral |
C) pentagon |
D) hexagon |
E) septagon |
SECTION-B
II. This section has Five questions. In each question a blank is left.
Fill in the blank. (5´ 2=10
MARKS)
1. The number of integral solutions of the equation x4-y4
= 2002 is _____
2. A,B,C,D are distinct and concyclic. 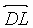 is perpendicular to
is perpendicular to 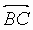 ,
, 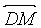 is
perpendicular to
is
perpendicular to 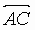 .
. 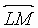 intersects
intersects 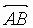 in N. The nonobtuse
angle enclosed between
in N. The nonobtuse
angle enclosed between 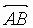 and
and 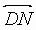 is _____ in degrees
is _____ in degrees
3. Let m be the 2002-digit number each digit of which is 6.
The remainder obtained when m is divided by 2002 is ______
4. If x is a real number Int.x denotes the greatest integer
less than or equal to x.
Int.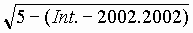 =
__________
=
__________
5. O is the origin and Pi is a point on the curve x2
+ y2 = i2 for any natural number i.
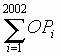
= OPj,
where j = _________
SECTION-C
III. This section has Five questions. Each question has a
short answer. Elegant solutions will be rewarded. (5´
2=10 MARKS)
1. If m is the right most nonzero digit of (n!)4
where n is a positive integer greater than 1, determine the possible values of
m.
2. Sketch the graph of the function f(x) = 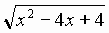 ,
, 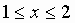 .
.
3. 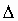 ABC is
right angled at A. AB=60, AC=80, BC=100 units. D is a point between B and C
such that the triangles ADB and ADC have equal perimeters. Determine the
length of AD.
ABC is
right angled at A. AB=60, AC=80, BC=100 units. D is a point between B and C
such that the triangles ADB and ADC have equal perimeters. Determine the
length of AD.
4. Do there exist positive integers p, q, r such that 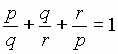 ?
?
5. k is a constant, (xi,0) is the mid point of (i-k,
0) and (i+k, 0) for i=1,2,…,2002 then find 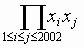 .
.
SECTION-D
IV. This section has Five questions. These questions are
long answer questions. Elegant solutions will be rewarded. (5´
6=30 MARKS)
1. If m and n are natural numbers such that
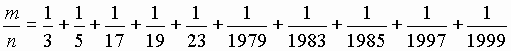 .
.
Prove that 2002 divides m.
2. 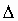 ABC is
right angled at A. Prove that the three mid points of the sides and the foot
of the altitude through A are concyclic.
ABC is
right angled at A. Prove that the three mid points of the sides and the foot
of the altitude through A are concyclic.
3. Determine all possible finite series in GP with first
term 1, common ratio an integer greater than 1 and sum 2002.
4. A convex pentagon ABCDE has the property that the area
of each of the five triangles ABC, BCD, CDE, DEA, and EAB is unity. Prove that
the area of the pentagon is 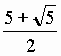 .
.
5. If a,b,c, are real numbers such that the sum of any two
of them is greater than the third and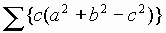 =3abc,
then prove that a=b=c.
=3abc,
then prove that a=b=c.
6. Explain how you will construct a triangle of area equal
to the area of a given convex quadrilateral. Use only rough sketches and give
proof.
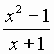 if x
if x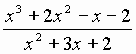 if x
if x![]() also
is a chord of a different circle with center C2 and radius r2.
S denotes the statement: The arc AB divides the first circle into two parts of
equal area.
also
is a chord of a different circle with center C2 and radius r2.
S denotes the statement: The arc AB divides the first circle into two parts of
equal area.![]() m where the line
segment l is a side of T1 and the line segment m is a side of T2,
whenever l
m where the line
segment l is a side of T1 and the line segment m is a side of T2,
whenever l![]() m is a unique point.
These points of intersection determine a convex polygon, which is a
m is a unique point.
These points of intersection determine a convex polygon, which is a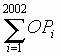
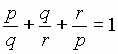 ?
?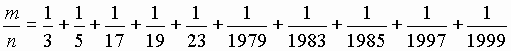 .
.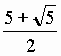 .
.