MATHEMATICS

Time: Two Hours
(8.30 AM - 10.30 AM)

 Max. Marks: 60

NOTE:-

  1. Answers must be written in English or the medium of instruction of the candidate in High school.
  2. Answer to each question should begin on a fresh page, and rough work must be enclosed with answer book.
  3. Attempt all questions.
  4. There is no negative marking.
  5. Answer all parts of a question at one place.
  6. Use of calculators, slide rule, graph paper and logarithmic, trigonometric and statistical tables is not permitted

Note:- All answers to questions in Section-A, Section-B, Section-C must be supported by mathematical arguments unless explicitly exempted.

SECTION-A

I. This section has Five questions. Each question is provided with five alternative answers. Only one of them is the correct answer. Indicate the correct answer by A,B,C,D,E. Order of the questions must be maintained. (5x2 =10 MARKS)

1. D ABC has integral sides AB, BC measuring 2001 units and 1002 units respectively. The number of such triangles is

A) 2001 B) 2002 C) 2003  D) 2004 E) 2005

2. Let m = 2001!, n = 2002 x 2003 x 2004. The LCM of m and n is

A) m B) 2002m C) 2003m  D) mn E) None 

3. The sides of a right-angled triangle have lengths, which are integers in arithmetic progression. There exists such a triangle with smallest side having length of

A) 2000 units B)  2001 units C) 2002 units  D)2003 units E) 1999 units

4. Let S be any expression of the form ek2k, where each ek is varied independently between 1 and –1. The number of expressions S such that S=0 is  

A) 0 B) 1 C) 2  D)22001 units E)None

5. Let a1, a2,….,a2001 be the lengths of the consecutive sides of a convex polygon P1, which is cyclic. Let b1, b2,…., b2001 be a permutation of the numbers a1, a2,…., a2001. Let P2 be a polygon with consecutive sides having lengths b1, b2,…., b2001. Then P2 is cyclic

A.  always
B. only if a1 = b1, a2 = b2,…., a2001 = b2001
C. only if b1, b2,…., b2001 is a cyclic permutation of a1, a2,…., a2001
D. only if the center of the polygon P1 lies in its interior
E. none of these

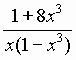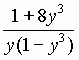SECTION-B

II. This section has Five questions. In each question a blank is left. Fill in the blank. (5x2 =10 MARKS)

1. n is the smallest positive integer such that (2001 + n) is the sum of the cubes of the first m natural numbers. Then m = _________, n = _________.

2. An equilateral triangle is circumscribed to and a square is inscribed in a circle of radius r. The area of the triangle is T and the area of the square is S. Then ________.

3. The smallest positive integer k such that (2000)(2001)k is a perfect cube is____________.

4. ABCD is a rectangle with AB = 16 units and BC = 12 units. F is a point on and E is a point on such that AFCE is a rhombus. Then EF measures _________units.

5. n is a positive integer not exceeding 9. The list of all n such that 10 divides nn – n is _____________________.

SECTION-C

III. This section has Five questions. Each question has a short answer. Elegant solutions will be rewarded. (5x2 =10 MARKS)

1. Given a set of ‘n’ rays in a plane, we mean by ‘a reversal’ the operation of reversing precisely one ray and obtaining a new set of ‘n’ rays. Starting from 2001 rays and performing one million reversals, is it possible to reverse all the rays?

2. If x + y+ z = a, prove that x2 + y2 + z2 ³ .

3. Given the locations P, Q, R of the midpoints of AB, BC, CA of a triangle ABC, explain how you will construct triangle ABC. Use only rough sketches and give proof.

4. If for every x > 0 there exists an integer k(x) such that½ a0 + a1x + a2x2 + ….. + anxn½ £ ½ xk(x) - 1½ , then find the value of a0 + a1 + …… + an.

5. We know that we can triangulate any convex polygonal region. Can we ‘parallelogramulate’ a convex region bounded by a 2001-gon?

SECTION-D

IV. This section has Five questions. These questions are long answer questions. Elegant solutions will be rewarded (5x6 =30 MARKS)

1. Solve in positive integers the cubic x3 – (x+1)2 = 2001.

2. The product of two of the roots of x4 – 11x3 + kx2 + 269x – 2001 is –69. Find k.

3. a) AB, BC, CD are the consecutive sides of a cyclic polygon of equal angles. Prove that D BCA @ D BCD.
b) Deduce that if a cyclic (2n+1)-gon has all its angles equal, then all its sides must be equal.
c) Prove by means of an example that a cyclic 2n-gon need not be equilateral if it is equiangular.

4. If (1+2x)(1+2y) = 3, xy ¹ 0, then show that = .

5. a) is the common chord of two intersecting circles. A line through A terminates on one circle at P and on the other at Q. Then prove that is a constant.

b) If two chords of a circle bisect each other prove that the chords must be diameters.