SCHOLASTIC APTITUDE TEST 2000
MATHEMATICS
| Time: Two Hours |
Max. Marks: 60
|
- Answers must be written in English
or the medium of
instruction of the candidate in High school.
- Attempt all questions.
- Answer all the questions in the booklets provided
for the purpose. No pages should be removed from the
booklets.
- There is no negative marking.
- Answer all questions of section I at one place.
Same applies to section II. The remaining questions can
be answered in any order.
- Answers to sections I and II must be supported by
mathematical reasoning.
- Use of calculators, slide rule, graph paper and
logarithmic, trigonometric and statistical tables is not
permitted
Section
I
This section has 5
questions. Each question is provided with five alternative
answers. Only one of them is correct.
Indicate the correct answer by A or B or C or D or E. Order
of the questions must be maintained. (5x2=10 Marks)
- A1A2………..A2000
is a polygon of 2000 sides. P is a point in the
plane of the polygon which is equidistant from all the
vertices of the polygon. Then
| A) There is no such P |
B) There is exactly one such P |
| C) Either A or B |
D) The locus of P is a straight
line |
| E) The locus of P is a circle |
|
- Consider the
following expressions in a,b,c.
- The expressions
which are not perfect squares among E1,E2,E3
and E4 are
| A) E1,E3 |
B) E2,E3 |
C) E2,E4 |
D) E1,E4 |
E) E3,E4 |
- Three angles of
a convex polygon measure each p /3 radians. Let n be the
number of sides of the polygon. Then
| A) The hypothesis is not
sufficient to evaluate n |
| B) n=3 |
C) n=6 |
D) n=9 |
E) None of these |
- There are n rods,
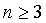 . The ith
rod has length 2i units. The number of closed
convex polygonal frames that can be made by joining the
rods end – to – end is
. The ith
rod has length 2i units. The number of closed
convex polygonal frames that can be made by joining the
rods end – to – end is
| A) 0 |
B) n |
C) n! |
D) nn |
E) 2n-1 |
- Integers from 1 to 2000
are written. A single operation consists of cancelling any
two of the numbers and replacing them by their
product. After 1999 such operations
A) No number will be left
B) Precisely 2 numbers will be left
C) More than two numbers may be left
D) Only one number will be left and it is 2000!
E) Only one number will be left, but it cannot be
uniquely determined
Section
II
This section has 5
questions. Each question is in the form of a statement with a
blank. Fill the blank so that the statement is true. Maintain the
order of the questions. (5x2=10 Marks)
- All possible 2000-gons
are inscribed in a circle of perimeter p. Let X=
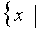 an
inscribed polygon has a side of length x.
an
inscribed polygon has a side of length x.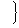 .
Then the greatest member of X is ____________ .
.
Then the greatest member of X is ____________ .
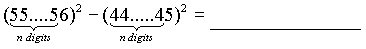
- Triangle ABCThe altitude
through A has length h. is right angled at A. Then
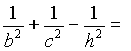
- p is a prime, n
a positive integer and n+p =2000. LCM of n
and p is 21879. Then
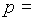 ______________ and
______________ and 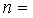 .
.
- The units digit of
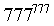 is _________.
is _________.
Section III
This
section has 5 questions. The solutions are short and methods,
easily suggested. Very long and tedious solutions may not get
full marks. (5x2=10 Marks)
- Does there
exist a right angled triangle with integral sides such
that the hypotenuse measures 2000 units of length?
- If a,b,c are not all
equal and (a+b+c)>0, determine the sign of a3+b3+c3-3abc.
- If real numbers x,y,z
satisfy
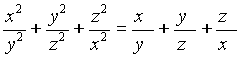 , then prove that x=y=z
, then prove that x=y=z
- Write down the solutions
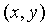 of
of 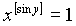 ,if x
>0 and
,if x
>0 and 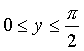 and
and
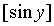 denotes
the integral part of
denotes
the integral part of 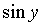
- Given
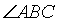 and a point D
in its interior. The problem is to find E
on
and a point D
in its interior. The problem is to find E
on 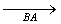 and F
on
and F
on 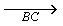 such
that D is the mid point of line segment
such
that D is the mid point of line segment 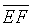 . A student
suggests the following method of construction: Join BD
and extend it to B’ such that BD = DB’.
Draw parallel to
. A student
suggests the following method of construction: Join BD
and extend it to B’ such that BD = DB’.
Draw parallel to 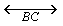 through B’. Take for E the
point where this parallel cuts
through B’. Take for E the
point where this parallel cuts 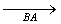 . Join ED and produce it to meet
. Join ED and produce it to meet 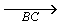 .Take for F
this point of intersection.
.Take for F
this point of intersection.Discuss the validity or
otherwise of this method of construction.
Section IV
This section has 5
questions. The solutions involve either slightly longer
computations or subtler approaches. Even incomplete solutions may
get partial marks.
- Consider the
equation in positive integers
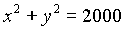 with
with 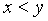 .
.
a) Prove that 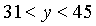 .
.
b) Rule out the possibility that one of 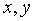 is even and the
other is odd.
is even and the
other is odd.
c) Rule out the possibility that both 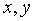 are odd.
are odd.
d) Prove that 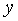 is a multiple of 4.
is a multiple of 4.
e) Obtain all the solutions. (10 Marks )
- ABCD is a trapezium with
AB and CD as parallel sides. The diagonals intersect at O.
The area of the triangle ABO is p and that of the
triangle CDO is q. Prove that the area of the
trapezium is
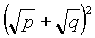 . ( 5 Marks )
. ( 5 Marks )
- Manipulate the equality
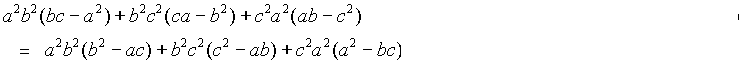
until the equlity 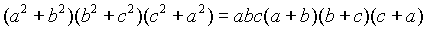 is obtained ( 5 Marks )
is obtained ( 5 Marks )
- If a triangle and a
convex quadrilateral are drawn on the same base and no
part of the quadrilateral is outside the triangle, show
that the perimeter of the triangle is greater than the
perimeter of the quadrilateral. ( 5 Marks )
- If a line parallel to,
but not identical with, x- axis cuts the graph of
the curve
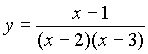 at
at 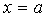 ,
,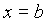 ,
then evaluate
,
then evaluate 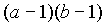 ( 5 Marks )
( 5 Marks )
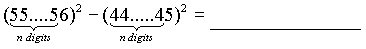
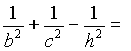
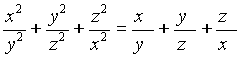 , then prove that x=y=z
, then prove that x=y=z 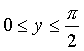 and
and
is obtained ( 5 Marks )
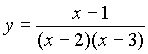 at
at